sin:
正弦值是在直角三角形中,对边的长比上斜边的长的值。 任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值
中文名:正弦值
外文名:sine function
应用学科:数学,物理,建筑学等
汉语发音:zhèng xían zhí
类别:函数
定义:弦值是在直角三角形中,对边的长比上斜边的长的值。 任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值,通常用符号sin表示。正弦sinθ也可以理解为顶角度数为θ的单位等腰三角形与单位等腰直角三角形的面积之比 。
sin30°=1/2
sin45°=√2/2
sin60°=√3/2
sin90°=1
sin180°=0
sin0°=0
sin270°=-1
其他公式
三角函数 必备公式:
Sin2A=2sinA·cosA
cos2A=cos^2A-sin^2A=1-2sin^2A=2cos^2A-1
tan2A=(2tanA)/(1-tan^2A)
同角三角函数的基本关系式
倒数关系; 商的关系;平方关系:
tanα ·cotα=1
sinα ·cscα=1
cosα ·secα=1 sinα/cosα=tanα=secα/cscα
cosα/sinα=cotα=cscα/secα sin2α+cos2α=1
1+tan2α=sec2α
1+cot2α=csc2α
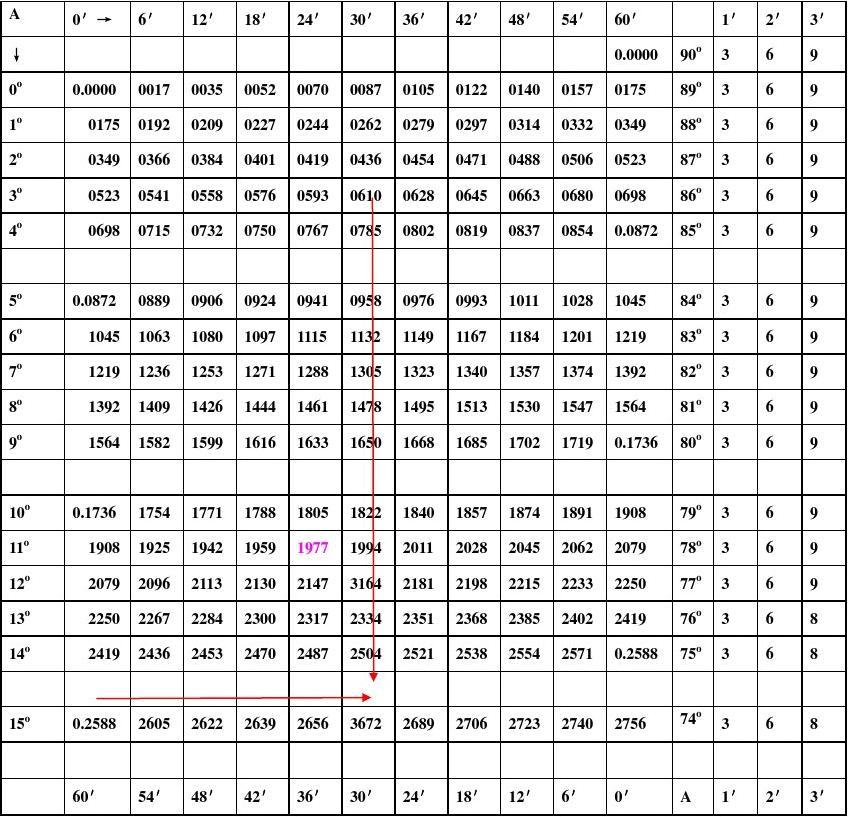
诱导公式
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
cot(-α)=-cotα
sin(π/2-α)=cosα
cos(π/2-α)=sinα
tan(π/2-α)=cotα
cot(π/2-α)=tanα
sin(π/2+α)=cosα
cos(π/2+α)=-sinα
tan(π/2+α)=-cotα
cot(π/2+α)=-tanα
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
cot(π+α)=cotα
sin(3π/2-α)=-cosα
cos(3π/2-α)=-sinα
tan(3π/2-α)=cotα
cot(3π/2-α)=tanα
sin(3π/2+α)=-cosα
cos(3π/2+α)=sinα
tan(3π/2+α)=-cotα
cot(3π/2+α)=-tanα
sin(2π-α)=-sinα
cos(2π-α)=cosα
tan(2π-α)=-tanα
cot(2π-α)=-cotα
sin(2kπ+α)=sinα
cos(2kπ+α)=cosα
tan(2kπ+α)=tanα
cot(2kπ+α)=cotα
(其中k∈Z)
万能公式
两角和与差的三角函数公式万能公式
sin(α+β)=sinαcosβ+cosαsinβ
sin(α-β)=sinαcosβ-cosαsinβ
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)
tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)
sinα=(2tan(α/2))/(1+tan2(α/2))
cosα=(1-tan2(α/2))/(1+tan2(α/2))
tanα=(2tan(α/2))/(1-tan2(α/2))
半角的正弦、余弦和正切公式 三角函数的降幂公式
二倍角的正弦、余弦和正切公式 三倍角的正弦、余弦和正切公式
sin2α=2sinαcosα
cos2α=cos2α-sin2α=2cos2α-1=1-2sin2α
tan2α=(2tanα)/(1-tan2α)
sin3α=3sinα-4sin3α
cos3α=4cos3α-3cosα
tan3α=(3tanα-tan3α)/(1-3tan2α)
三角函数的和差化积公式三角函数的积化和差公式
α+β α-β
·积化和差公式:
sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]
cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]
cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]
sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]
·和差化积公式:
sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]
sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]
cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]
cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]
常用函数数值
α=0°(0)
sinα=0
cosα=1
tαnα=0
cotα→∞
secα=1
cscα→∞α=15°(π/12)
sinα=(√6-√2)/4
cosα=(√6+√2)/4
tαnα=2-√3
cotα=2+√3
secα=√6-√2
cscα=√6+√2
α=22.5°(π/8)
sinα=√(2-√2)/2
cosα=√(2+√2)/2
tαnα=√2-1
cotα=√2+1
secα=√(4-2√2)
cscα=√(4+2√2)α=30°(π/6)
sinα=1/2
cosα=√3/2
tαnα=√3/3
cotα=√3
secα=2√3/3
cscα=2α=45°(π/4)
sinα=√2/2
cosα=√2/2
tαnα=1
cotα=1
secα=√2
cscα=√2α=60°(π/3)
sinα=√3/2
cosα=1/2
tαnα=√3
cotα=√3/3
secα=2
cscα=2√3/3α=67.5°(3π/8)
sinα=√(2+√2)/2
cosα=√(2-√2)/2
tαnα=√2+1
cotα=√2-1
secα=√(4+2√2)
cscα=√(4-2√2)α=75°(5π/12)
sinα=(√6+√2)/4
cosα=(√6-√2)/4
tαnα=2+√3
cotα=2-√3
secα=√6+√2
cscα=√6-√2α=90°(π/2)
sinα=1
cosα=0
tαnα→∞
cotα=0
secα→∞
cscα=1α=180°(π)
sinα=0
cosα=-1
tαnα=0
cotα→∞
secα=-1
cscα→∞α=270°(3π/2)
sinα=-1
cosα=0
tαnα→∞
cotα=0
secα→∞
cscα=-1α=360°(2π)
sinα=0
cosα=1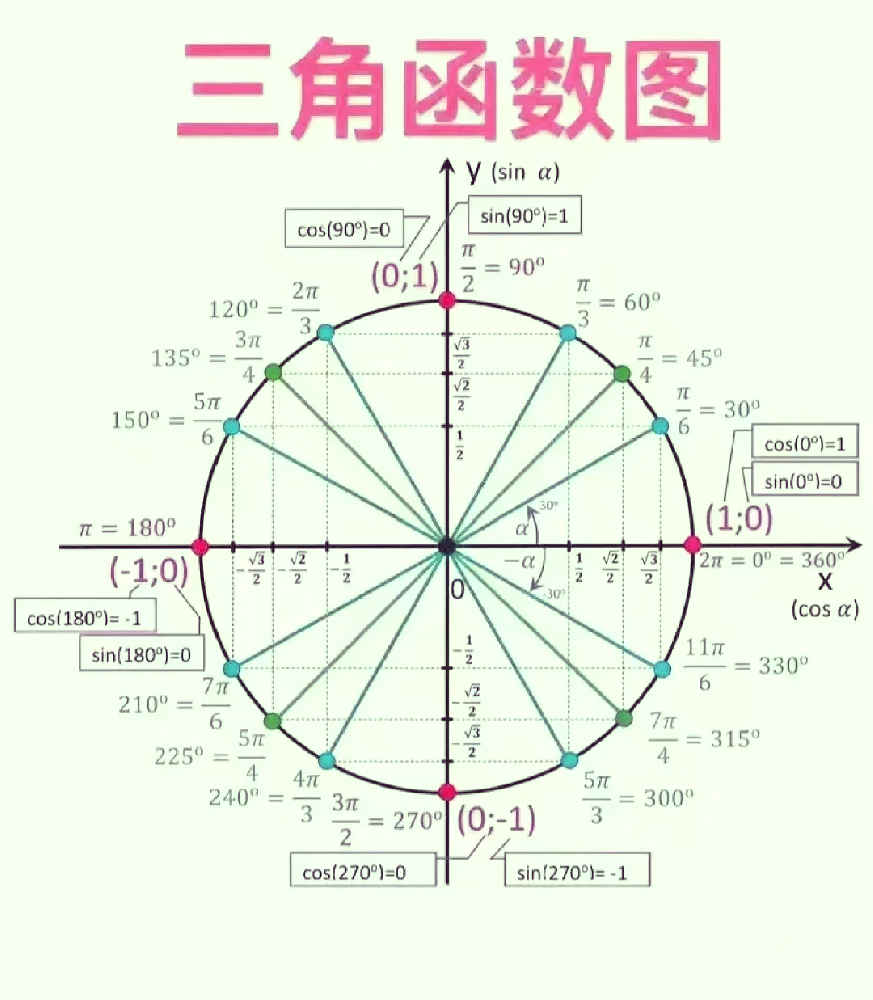
tαnα=0
cotα→∞
secα=1
cscα→∞
埃及的三角学
由公元前1650年前后由一位书吏抄录的“阿美斯纸草书”的第56题可知,当时的埃及人已经引入了一种类似于角的余切的概念。
希腊的三角学
早期的希腊人曾对一个圆里的角 (或弧)与其所对应弦长的关系做过系统研究。弦的属性,作为圆的中心角或内接角的度量,已经被希波克拉底时代的希腊人所熟悉。在欧几里得的作品中,没有严格意义上的三角学,而只有相当于某些特定三角学法则或公式的定理。
公元一世纪末至二世纪初,托勒密所做的《至大论》一书对于三角学有着更为透彻的阐释。该书的第一卷记载了托勒密编制的弦表,从至180°,每隔一项,精确到秒。这实际上就是从到90°、以的幅度递进的正弦表。
印度的三角学
公元四世纪至五世纪,印度数学家编写的《悉昙多》和《阿利耶毗陀论》中记载了现存最早的正弦关系表。这些表给出了直至90°角的正弦,每隔一项,共24项。
其他网址:
https://vd3.bdstatic.com/mda-kaisjaiiiwctykx4/v1-cae/hd/mda-kaisjaiiiwctykx4.mp4
https://vd3.bdstatic.com/mda-kaht852kyec76cz2/v1-cae/hd/mda-kaht852kyec76cz2.mp4
https://vd3.bdstatic.com/mda-mehqtg32z4gasuw6/hd/cae_h264/1621359687899962133/mda-mehqtg32z4gasuw6.mp4
https://vd3.bdstatic.com/mda-kaisjaiiiwctykx4/v1-cae/hd/mda-kaisjaiiiwctykx4.mp4
https://www.baidu.com/s?key=%E7%99%BE%E5%BA%A6&wd=%E6%AD%A3%E5%BC%A6%E5%80%BC
https://baike.baidu.com/item/%E6%AD%A3%E5%BC%A6%E5%80%BC/10802586?fr=aladdin
https://vd3.bdstatic.com/mda-pmj1t16vvk8108v8/hd/cae_h264/1703054192150210491/mda-pmj1t16vvk8108v8.mp4